• Introdução histórica
• A escala linear vs dimensões reais
• A escala de superfície / Área
• A escala volumétrica
• Outros

Fabrico de soldadinhos de chumbo

Com a revolução industrial começaram a ser fabricados em série os primeiros brinquedos. Estava então muito na moda entre as classes altas da sociedade, as bonecas e casinhas de bonecas para as raparigas e os soldadinhos de chumbo e os comboios (que entretanto tinham começado a ser utilizados) para os rapazes.

Deve-se sobretudo aos alemães a produção maciça de soldadinhos de chumbo. Os moldes em que eram feitos eram fáceis de confecionar e o metal fácil de fundir. Depois era só desenformar e pintar.

Com o tempo alguns vendedores começaram a aperceber-se que muitos compradores adquiriam facilmente soldadinhos de chumbo de diferentes fabricantes, desde que tivessem tamanhos harmoniosos entre eles. Assim, para fomentarem as vendas, começaram a exigir tamanhos padronizados aos fabricantes.

Colocava-se então uma questão importante: Que tamanho deveriam ter os bonecos?

Uma medida facilmente percebida e processada pelo cérebro humano é o tamanho de um homem. Ou seja, se colocarmos um soldadinho de chumbo ao lado de uma carroça puxada por cavalos ou o mesmo soldadinho ao lado de um pequeno barco, facilmente temos uma ideia das proporções tidas por reais dos objetos, desde que as escalas dos diferentes modelos sejam harmoniosas entre si. Logo o tamanho do ser humano era uma excelente referência.

Sabemos que as medidas inicialmente utilizadas para o cálculo de escalas eram as do sistema de medida inglês, nomeadamente o pé e a polegada. Multiplicando um pé (1 pé = 30,48 cm) por seis, dá que 6 pés (ou 182,88 cm) são uma medida muito próxima do tamanho médio de um homem.

Dividindo esse valor por uma polegada (2,54 cm) dá 72. Nascia assim a primeira escala estandardizada. A evolução desta escala, tida por alguns como muito pequena, deu origem em pouco tempo a outras escalas, em que os mesmos princípios foram seguidos.

6’ (182,88cm) a dividir por 1’’ (2,54cm) = 72 -> Escala 1:72 -> 1 homem = 2,54cm

Assim, aplicando múltiplos temos escalas cada vez mais pequenas, mas em contrapartida kits (desde que do mesmo modelo a reproduzir) cada vez maiores e mais detalhados.

6’ (182,88cm) a dividir por 1’’ (2,54cm) = 72 -> Escala 1:72 -> 1 homem = 2,54cm

6’ (182,88cm) a dividir por 1.5’’ (3,81cm) = 48 -> Escala 1:48 -> 1 homem = 3,81cm

6’ (182,88cm) a dividir por 2.25’’ (5,71cm) = 32 -> Escala 1:32 -> 1 homem = 5,71cm

6’ (182,88cm) a dividir por 3’’ (7,62cm) = 24 -> Escala 1:24 -> 1 homem = 7,6 cm

6’ (182,88cm) a dividir por 4’’ (10,16cm) = 18 -> Escala 1:18 -> 1 homem =10,16 cm

Aplicando submúltiplos temos, pelo contrário, escalas cada vez maiores, mas em contrapartida kits (desde que do mesmo modelo a reproduzir) cada vez menores e menos detalhados.

6’ (182,88cm) a dividir por 0.5’’ (1,27cm) = 144 -> Escala 1:144 -> 1 homem = 1,27cm

Mas para reproduzir objetos extraordinariamente grandes em que a referência “homem” não faz sentido, foram criadas as escalas 1:200, 1:350, 1:400, 1:700, 1:750, 1:1000, 1:2000, entre muitas outras.

Com o aparecimento no mercado de modelos produzidos por firmas (sobretudo francesas) que utilizam o sistema métrico decimal (SMD), surgem novas escalas, algumas delas muito idênticas a algumas já existentes. São exemplo as escalas 1:76, 1:35 e 1:25. Estas escalas são tão próximas, respetivamente das 1:72; 1:32 e 1:24, que se num diorama forem utilizados kits das diferentes escalas, o resultado não será muito agressivo ao olhar.

Há quem defenda que estas novas escalas se devem sobretudo ao facto de a França e outros países europeus não quererem adotar as medidas anglo-saxónicas entretanto padronizadas; outros defendem que a utilização das medidas em pés e polegadas não são de fácil compreensão para quem utiliza diariamente o sistema métrico. Há ainda outros que defendem que é uma questão de arredondamento, em que 1’= 30cm e 1’’= 2,50cm.

Mas esta ultima justificação não convence muito, sobretudo porque, em rigor, não se obtêm esses valores de escala por arredondamento, nem justificam o constante aparecimento de novas escalas atípicas sobretudo produzidas por estes países, nomeadamente 1:50, 1:60, 1:130, 1:150 entre outras.

Relativamente ao ferromodelismo a escala é encontrada tendo por referência a bitola (distancia entre os trilhos) e é apresentada num sistema alfabético ou alfanumérico (N, HOn3, HO, S,…). Mas como não percebo muito do assunto não me vou alargar antes que dê asneira. Já relativamente ao automodelismo (tanto com motor de combustão como com motor elétrico) as escalas mais usadas são as 1:8 e 1:10. Quanto ao autorama (pistas de carros) as escalas mais usuais são a 1:32 para lazer e a 1:24 para competição.

No nautimodelismo e aeromodelismo a escala não é rígida e está geralmente associada a questões relacionas com a flutuabilidade e a aviónica ou à necessidade de espaço para instalação e montagem dos componentes mecânicos necessários.

A escolha da escala é muito importante e algumas variáveis devem ser tidas em conta:

Espaço: Se é como eu e não se consegue “desfazer” de um trabalho realizado por si, com o tempo o espaço para arrumo dos trabalhos finalizados começa a ser um problema, por isso esta é uma variável muito importante.

Oferta: Se quer iniciar uma coleção numa determinada escala, por exemplo caças da II guerra mundial, veículos militares da guerra do Golfo, ou qualquer outra, deve ter em consideração a oferta de kits existentes no mercado, pois se optar por uma escala com poucos produtos corre o risco de limitar a sua coleção.

Opções: Esta é igualmente uma variável muito importante, pois um projeto em modelismo é mais do que montar um kit. É necessário ter em conta os upgrades disponíveis no mercado que nos permitirão enriquecer o kit em que estamos a trabalhar. Mas também poderemos querer enriquecer o cenário/diorama em que o vamos colocar com outros elementos à mesma escala (Figuras, edifícios, plantas, …), por isso para além da escolha das escalas do kit, também temos que verificar se existem opções de enriquecimento para o nosso projeto na escala em que estamos a trabalhar.

Comparação de tamanhos		Comparação entre escalas iguais
A - Figura de um elemento da tripulação de tanque alemão à escala 1:35. Multiplicando 5.100 cm por 35 obtemos 178.5 cm, ou seja 1.78 metros, o que corresponde a uma altura “normal” para um homem. B – Figura de um mecânico americano da USAF à escala 1:72. Multiplicando 2.250 cm por 72 obtemos 162 cm, ou seja 1.62 metros, o que corresponde a um homem relativamente pequeno, mas dentro dos limites normais.		A Figura “A” mede 2.250 cm e a figura “B”2.550 cm, ambas à escala 1: 72. Se multiplicarmos estes valores por 72, obteremos respetivamente 162 cm e 183.6 cm, ou seja 1,62 metros e 1.83 metros. Valores bastante diferentes mas perfeitamente dentro dos padrões. O importante mesmo é nunca usar figuras com dimensões absurdas relativamente à escala que estamos a usar. Por isso convém fazer alguns cálculos rápidos como os aqui apresentados, pois por vezes há fabricantes que lançam produtos com as dimensões erradas. Este principio é valido tanto para figuras como para os próprios kits.

A escala linear tem algumas limitações, nomeadamente não se poder aplicar para objetos com mais do que uma dimensão.

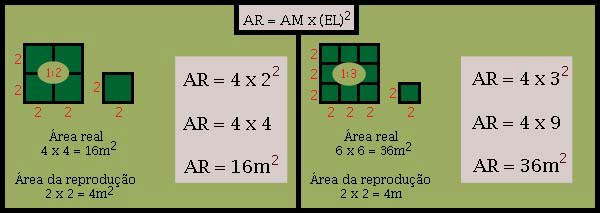
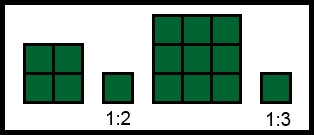
Observando a figura ao lado facilmente se compreende que a área da figura à escala linear 1:2 corresponde a 1:4 da figura original. Mas a escala linear 1:2 também está correta, pois o comprimento da reprodução é metade do objeto tido por real, daí 1:2. Esta propriedade é válida para qualquer objeto independentemente da sua forma.

Então coloca-se uma questão. Como calcular a escala de superfície/área de um determinado objeto?

A escala de superfície/área do objeto real é igual à área do modelo multiplicada pela escala linear elevada ao quadrado ou seja:

Fórmulas possíveis:   AR = AM x (EL)2 AM = AR / (EL)2 EL = (Raiz quadrada de (AR : AM))

De onde: AR - Área real do modelo AM - Área do modelo reproduzido EL - Escala linear utilizada